今天青果君想與你分享一種認知管理方法，也是一種學習方法：以教為學，通過教別人來學習。

用自然的語言，傳遞枯燥且有價值的知識，仿佛踩著高蹺起舞，這并不容易。事實上，令人抓狂的數學題，也是可以用深入淺出的方式講明白的。

諾貝爾獎物理學獎獲得者，原子彈之父費費曼就是這方面的高手，費曼說，最好的學就是給別人講。

所謂“費曼學習法”：通過向別人清楚地解說一件事，來確認自己真的弄懂了這件事。

不知你意識到沒有，從古到今，全世界最牛的知識內容，都是以對話的形式存在的。

想想你腦海中的“子曰：學而時習之，不亦說乎”，就明白了。東方的孔子，西方的蘇格拉底就是這方面的集大成者。

為什么說，教是最好的學？

有時候，我們要講一個概念，覺得很簡單了，但在落筆的時候發現根本沒辦法把它用明確簡單的話陳述出來——你說不清楚，實際上是因為你沒理解這個概念。

①當你要去教別人的時候，會啟動一種“保護效應機制”——你要保護自己的正確性，你要調動全部的知識和能力，讓自己越過一個個邏輯漏洞。

②你教他的時候會想到一系列問題，比如“解這道題最簡便的方法是什么？”，“如果概念解釋不清楚，能不能用更簡單的方法呢？”，這就需要你有一種打通知識和觸類旁通的能力，或者說是一種知識融通的能力。

③“他會怎么理解這個概念”，“要想讓他懂，關鍵點和結論是什么，如何論證，最難的是什么”。當你不斷這樣思考去輔導別人的時候，它會迫使你的表述盡可能地主動和具有創造性。

④在教別人過程中，通過別人的疑問、質疑、無視和新想法，會讓我們對問題的認識更全面，有助于跳出固有思維模式。

⑤教別人學的過程其實是一種高強度的自學過程，你被迫去補各種各樣的知識漏洞，橫向、縱向擴展你的知識面，打通知識體系。

⑥根據艾賓浩斯遺忘曲線，教別人的過程，是一個強化重復記憶的過程，而且場景化知識更容易記住。

亞里士多德說，“哲學起源于好奇”，這個“好奇”一是興趣，二是疑問：先有了問題才可能學習。換句話說就是：提取是最好的存儲。

通過教別人，“提取”出一系列問題，接下來就是一個填坑的過程。所以，教別人與其說這是學習的過程，不如說是一個補習的過程。

第一步 - 選擇一個你想要理解的概念，最好用思維導圖的形式表現出來。

第二步 - 設想一種場景，你正要向別人傳授這個概念

第三步 - 如果你感覺卡殼了, 就回顧一下學習資料

第四步 - 為了讓你的講解通俗易懂，簡化語言表達

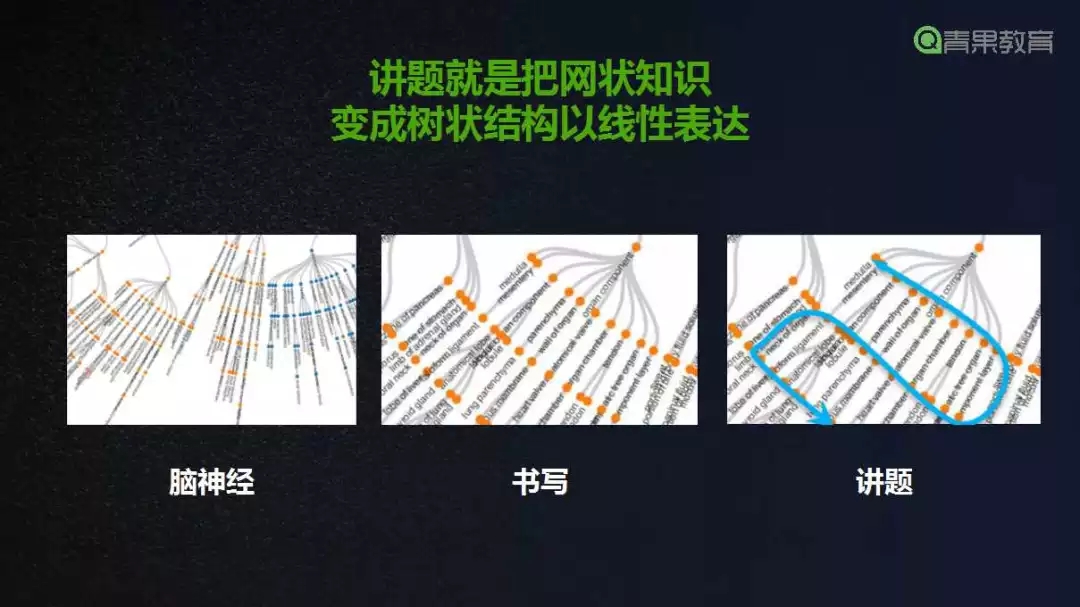
注：圖片來自古典

當我們把所有的概念都弄清楚之后，用自己的話，把這個道題解法重新講一遍， 只要別人能聽懂你說的意思，那就說明你自己的學習成功了。

以教為學的過程中，會促使你更多的去思考，并且把基礎知識做到了融會貫通。這也是一個刻意練習的過程。

文 青果教育整理發布，轉載請注明出處