開篇之前，

我想問你一個問題：

如何用數學的方法表白？

文學家們用文字，音樂家們用旋律，至少這些還是我們可以理解的，周圍一堆數學高手，好奇那些看著乏味的數學家們會如何表白呢？

據說在1650年的斯德哥爾摩街頭，笛卡爾52歲時邂逅了18歲的瑞典公主克里斯汀，他成了公主的數學老師。

后來，笛卡爾被流放回法國，總共給公主寄出過13封情書，也就是在最后一封信中，只有短短的一個數學公式：r = a(1-sinθ)

你知道它是什么意思嗎？

而這位公主呢，她恰好是個低調的數學迷，她一眼就看破了其中真意，于是優雅的在紙上，在直角坐標系中將曲線畫了出來，于是一個心形圖案躍然紙上。

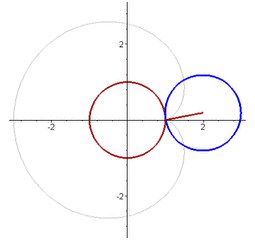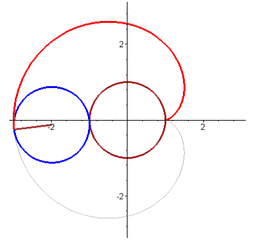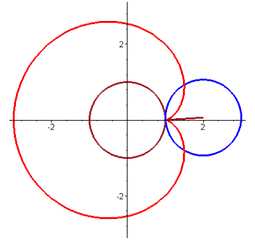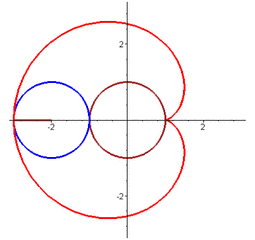
這封享譽世界的另類情書，至今，還保存在歐洲笛卡爾的紀念館里。浪不浪漫！有沒有一種數學家獨特的浪漫，是不是另一種不同的美！是不是對數形結合有了一個感性的認識？

具體講數形結合思，想就不得不再說道上文中的——“笛卡爾”，自從歐幾里德的《幾何原本》問世以來，人們一直把代數限定在研究數及其關系的范疇內，把幾何限定在研究位置和圖形的范疇內。

代數和幾何截然分家持續了幾千年，猶如兩座高山被萬丈深淵分割，連接代數和幾何的橋梁將“數”和“形”緊密聯系在一起的科學就是笛卡兒創立的坐標幾何學，數形結合思想就此產生。

數學思想方法可以說是數學的靈魂和精髓，而數形結合思想是數學解題當中最常用、最重要的數學思想方法之一，也是初中學生必須嫻熟掌握的數學技能之一。

數與形是數學中兩個最古老、最基本的元素，是數學大廈深處的兩塊基石，所有的數學問題都是圍繞數和形的提煉、演變、發展而展開的：每一個幾何圖形中都蘊藏著一定的數量關系，而數量關系又常常可以通過圖形的直觀性作出形象的描述。

因此，在解決數學問題時，常常根據數學問題的條件和結論之間的內在聯系，將數的問題利用形來觀察，提示其幾何意義；而形的問題也常借助數去思考，分析其代數含義。

如此將數量關系和空間形式巧妙地結合起來，并充分利用這種“結合”，尋找解題思路，使問題得到解決的方法。

簡言之，就是把數學問題中的數量關系和空間形式相結合起來加以考察的處理數學問題的方法，稱之為數形結合的思想方法。

我國著名數學家華羅庚曾說:“數缺形時少直觀，形少數時難入微；數形結合百般好,隔離分家萬事休”。

數形結合就是把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來, 通過"以形助數"或"以數解形"即通過抽象思維與形象思維的結合，可以使復雜問題簡單化，抽象問題具體化，從而起到優化解題途徑的目的。

數形結合的思想方法是數學學習的主線之一，應用數形結合的思想解題，不僅直觀易于尋找解題途徑，而且能避免繁雜的計算和推理，簡化解題過程。具體可以解決以下問題:

在運用數形結合思想分析和解決問題時，要注意三點：

作為一種 數學思想方法，數形結合的應用大致又可分為兩種情形：

換句話說，數形結合包括三個方面：以數化形、以形變數、形數互變。

由于“數”和“形”是一種對應，有些數量比較抽象，我們難以把握，因此我們可以把“數”的對應“形”找出來，利用圖形來解決問題。

雖然形有形象直觀的優點，但在定量方面還必須借助代數的計算，充分利用圖形的性質或幾何意義，把“形”正確表示成“數”的形式，進行分析計算。

在有些數學問題中不僅僅是簡單的“以數變形”或“以形變數”而是需要形數互相變換，不但要想到由形的直觀變為“數”的嚴密還要由“數”的嚴密聯系到"形"的直觀。

總之，數形結合是將抽象的數學語言與直觀圖形結合起來，不僅能直觀地發現解題的途徑，而且能避免復雜的計算與推理，大大簡化解題的過程。

4、中學考點分析

在初中數學中數形結合思想貫穿整個教材的始終，諸如：在學習二次函數、代數、三角形等問題中都運用到了數與形狀的結合。

可以說數形結合的思想方法是解決初中數學問題乃至高中、大學、等等數學問題的一個通法，運用一秒存乎一心。

在做題中，要重視“數形結合”的思維訓練，只要與“形”沾得上一點邊，就應該根據題意畫出草圖來分析一番。

這樣做，不但直觀，而且全面，整體性強，容易找出切入點，對解題大有益處。

下面，青果教育研究院院長常性軍老師結合具體考點，針對“數形結合”思想的具體運用，特別設計了這些經典題型，與你分享。希望同學們可以認真理解，做一道題，學會一類題，一步行，千里亦能行。

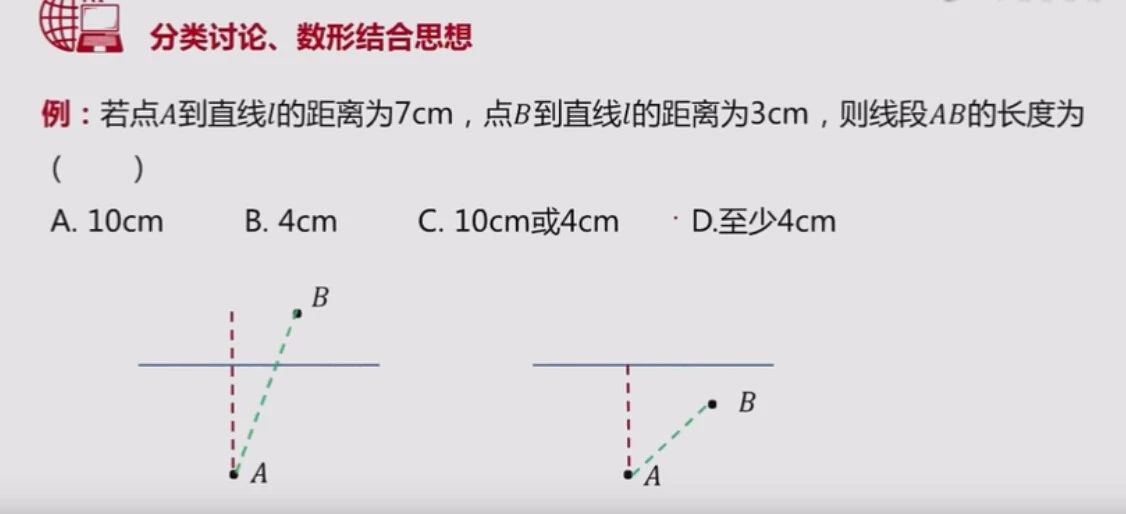
總而言之，數形結合，是初中生不得不跨的坎，無它，因為數形結合在某種程度上來說是數學解題的捷徑和鑰匙，掌握了數形結合的思想，提高30分不是夢。

希望借此文讓大家能認識到數形結合思想在中學數學解題中的重要性，對數學學習有所幫助！