分類討論思想
學習方法 | 05-16 15:54 13105次 8次
麥肯錫有個分類法則,叫MECE法則。中文意思是“相互獨立、完全窮盡”。簡單來說,就是使用MECE法則分類,各個要素之間要保證不能有交叉,也不能有遺漏,也就是“不重不漏”。

舉個例子,把人分為男人和女人,就符合MECE法則。因為從人的生理結構上來說,除了男人就是女人。
但如果把人分為男人和未婚女人,就有問題了,因為沒有窮盡,把已婚女人給遺漏了;把人分為男人和已婚人士,又出現了重復,因為男人里邊有已婚的,已婚里邊有男人。
在信息分類的時候,MECE就好比一把尺子,可以用來判斷信息要素是不是分類清楚了。
是不是覺得這個法則特別實用,其實它只是分類討論數學思想在實際工作生活中的一種應用方式。
分類討論思想
所謂分類討論,就是在研究和解決數學問題時,當問題所給對象不能進行統一研究,我們就需要根據數學對象的本質屬性的相同點和不同點,將對象區分為不同種類,然后逐類進行研究和解決,最后綜合各類結果得到整個問題的解決,這一思想方法,我們稱之為“分類討論的思想”。
簡而言之,就是把要研究的對象按照相同點和不同點分成各種不同情況分門別類加以討論,然后把各種情況討論出來的結果整合起來,是一種化繁為簡的思維過程,考察學生的思維縝密性和全面性。

對問題實行分類與整合,確定分類標準后等于增加了一個已知條件,實現了有效增設,將大問題分解為小問題,優化解題思路,降低問題難度。
分類討論的思想之所以重要,有四個原因:

一是它的邏輯性較強;二是它的知識點的涵蓋比較廣;三是它可培養學生的分析和解決問題的能力;四是實際問題中常常需要分類討論各種可能性。
分類的原則
分類討論也要遵循一定原則進行的,分類的對象是確定的,標準是統一的,每一部分是相互獨立的,既不重復、也不遺漏。

原則1:按統一標準劃分,比如,我們想知道班里的男生女生的平均身高,那么我們是不是要把班上所有學生分成男生,女生兩類,而這個分類標準是性別。
原則2:不重不漏,就是被分后的各種情況不能有重疊部分而且合起來是整個研究對象的全部,如男生中不能有女生,同樣,女生中不能有男生,而且男生加上女生要是全班的總人數。
原則3:按照等級先后順序進行,有時候我們做一次分類還不夠還需要對其中某些情況再分類。
常見的類型
類型1:由數學概念引起的的討論,如實數、有理數、絕對值、點(直線、圓)與圓的位置關系等概念的分類討論;
類型2:由數學運算引起的討論,如不等式兩邊同乘一個正數還是負數的問題;
類型3 :由性質、定理、公式的限制條件引起的討論,如一元二次方程求根公式的應用引起的討論;
類型4:由圖形位置的不確定性引起的討論,如直角、銳角、鈍角三角形中的相關問題引起的討論。
類型5:由某些字母系數對方程的影響造成的分類討論,如二次函數中字母系數對圖象的影響,二次項系數對圖象開口方向的影響,一次項系數對頂點坐標的影響,常數項對截距的影響等。
分類討論思想是對數學對象進行分類尋求解答的一種思想方法,其作用在于克服思維的片面性,全面考慮問題。
中學考點分析
應用分類討論的思想對問題求解,首先要明確討論對象,確定對象的全體;其次是確定分類標準,分層次,不重復,不遺漏,達到互斥、無漏、最簡的原則;
最后還要反思其過程,從中發現“分”與“合”,“局部”與“整體”之間的辨證統一關系,充分挖掘求解問題中潛在特殊性與簡單性,盡可能地簡化或避免分類討論;使解題思想得到進一步升華,使解題的途徑更加簡潔的策略。
鐺鐺鐺鐺~又到了青果送福利時間了,下面,青果教育研究院院長常性軍老師結合具體考點,針對“分類討論思想”的具體運用,特別設計了以下經典題型,與你分享。
希望同學們可以認真理解,做一道題,學會一類題,一步行,千里亦能行。
分類討論思想常見的六種類型
方程 若含有字母系數的方程有實數根時,要考慮二次項系數是否等于0,進行分類討論。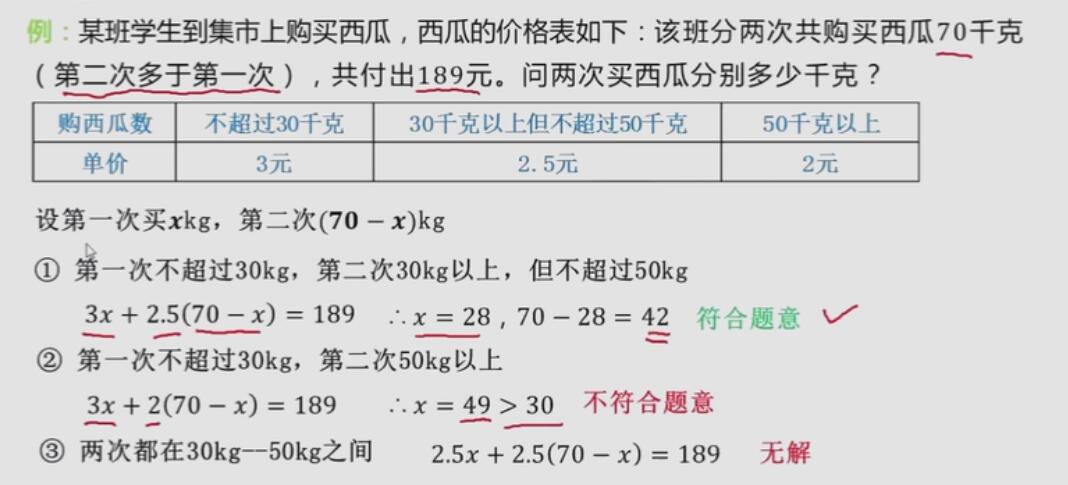
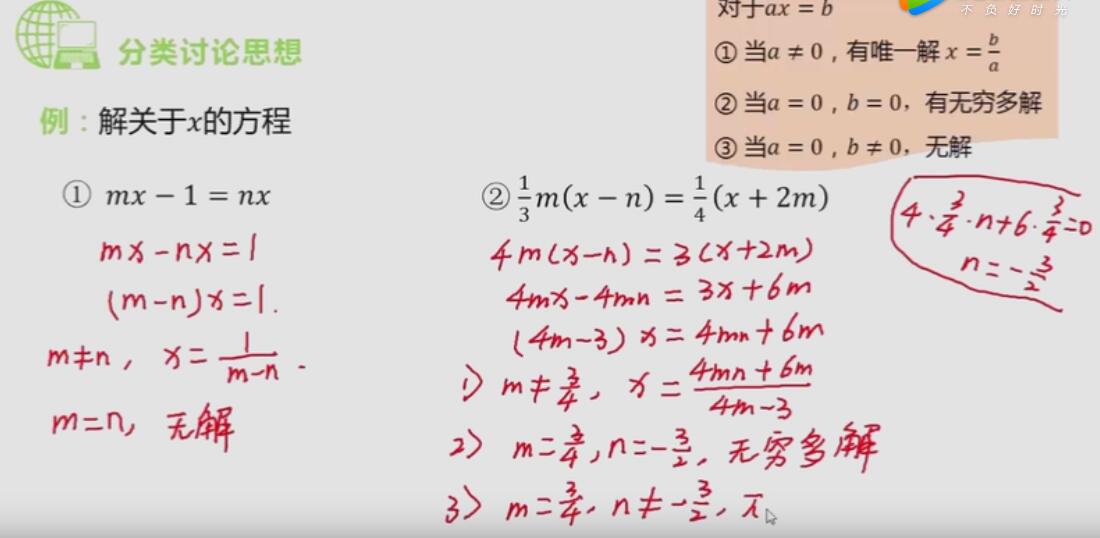
直角三角形 在直角三角形中給出兩邊的長度,確定第三邊時,若沒有指明直角邊和斜邊,要注意分情況進行討論(分類討論),然后利用勾股定理即可求解。

相似三角形 如果題目中出現兩個三角形相似,需要討論各邊的對應關系;若出現位似,則考慮兩個圖形在位似中心的同旁或兩旁兩種情況討論。 一次函數 已知一次函數與坐標軸圍成的三角形的面積,求k的值,常分直線交于坐標軸正半軸和負半軸討論;確定反比例函數與一次函數交點個數,常分一、三象限或二、四象限兩種情況討論。
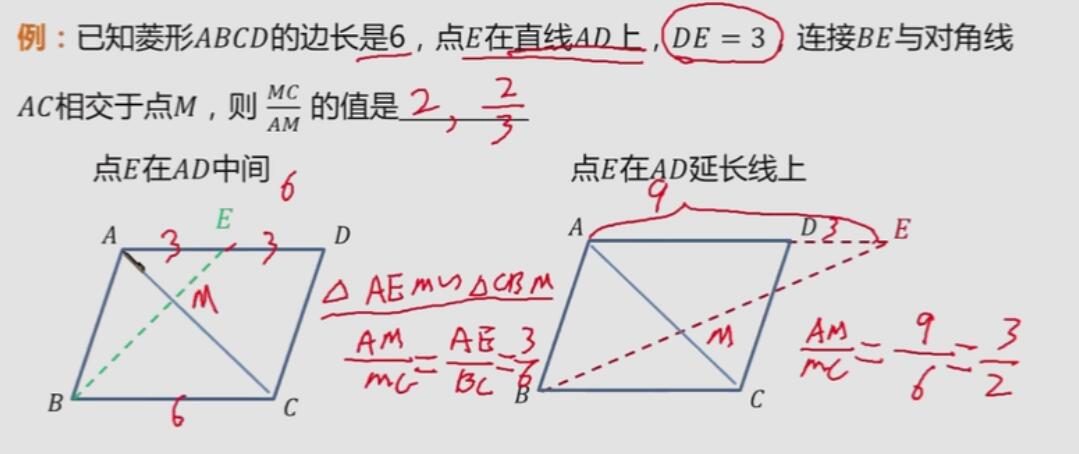



圓 圓的一條弦(直徑除外)對兩條弧,常分優弧和劣弧兩種情況討論;求圓中兩條平行弦的距離,常分兩弦在圓心的同旁和兩旁兩種情況討論;圓與圓的相切,此時要考慮分外切和內切兩種情況討論。

當數學問題中的條件,結論不明確或題意中含參數或圖形不確定時,就應分類討論。
總而言之,應用分類討論思想解決問題必須保證分類科學,標準統一,做到不重復,不遺漏,并力求最簡。
化繁為簡,破“簡”成蝶!
8人贊